Gamelan scales: Pelog and Slendro

In Indonesia there are musical ensembles, called gamelans, with weird tunings. It's wonderful. They don't have exact octaves. They have precise tuning within an ensemble but they vary widely between ensembles. They use inharmonic hammered metallophones with bell like timbres. Their scales are inharmonic. Everything about it is weird and wonderful and awesome.

I want to deeply understand Gamelan music. I'm going to approach this from many angles until something sticks.

One of the Gamelan scales is called Pelog. Some people will tell you it sounds like a subset of 9-EDO. It does sound like 9-EDO, but it's not 9-EDO. It has a wider octave, for example. Is it based on 9 equal divisions of a stretched octave? I'm not sure. I doubt it, because the intervals would still be equal, just equal at a different size, and they're not. But we'll look into it.

Do Gamelan scales minimize sensory dissonance of inharmonic resonators against each other or against a harmonic instrument? This might be part of it, but the metallophones sound pretty similar from region to region while the scales are noticeably different? But we'll look into it.

Before we look into those things, I just wanted to assume for a moment that the Pelog scale was harmonic, even though it's clearly not. I looked at a bunch of measured tunings for pelog scales from different gamelans, took averages in logarithmic frequency space, and tried to make sense of the scale that showed up that way as if the intervals were harmonic.

Here's my first stab at it:

Pelog scale, relative intervals:

    [ReSbAcM2, Prm2, ReSpAcA2, Prm2, m2, Asm2, AsM2] # [14/13, 13/12, 108/91, 13/12, 16/15, 11/10, 55/48] _ [128c, 139c, 297c, 139c, 112c, 165c, 236c]

Pelog scale, absolute intervals:

    [P1, ReSbAcM2, Sbm3, ReAcA4, P5, m6, AsGrd7, AsAsGrd8] # [1/1, 14/13, 7/6, 18/13, 3/2, 8/5, 44/25, 121/60] _ [0c, 128c, 267c, 563c, 702c, 814c, 979c, 1214c]

This has fairly simple frequency ratios and interval names in both the relative and absolute representations. The "ReSbAcM2" relative interval might not look very simple to you, but it's a Zalzalian neutral seconds from Persian/Ottoman/Arabic music theory, and I like it fine.

If you look at the relative scale degrees, you can see how they're fairly close to one or two steps of 9-EDO at 133 cents and 267 cents respectively. In so far as we could use 9-EDO the relative steps are:

     [1, 1, 2, 1, 1, 2, 1]

And the absolute steps are:

[0, 1, 2, 4, 5, 6, 8, 9]

i.e. we skip steps 3 and 7.

If we gave the scale tones traditional names, they would be 

    [low bem, gulu, dada, pelog, lima, nem, barang, high bem].

The other foundational scale in Gamelan is called Slendro. Some people will tell you that it sounds like 5-EDO. You might wonder, if Pelog sounds like 9-EDO and slendro sounds like 5-EDO, could we play Gamelan music in 9 * 5 = 45-EDO? I'm not sure. You could play something similar. In addition to their pseudo-octave being a stretched wide, I've heard that they don't have a notion of octave equivalence, but they at least have, like, low bem versus high bem. And some of their instruments have like 12 notes, so if the scales only have 5 and 9 notes respectively, there's got to be something like repetition of tones higher up or lower down, right?

Let's look at the tuning of slendro. Here are the measured tunings of 8 slendro scales from different regions, measurements by Jaap Kunst, as presented in "Interval Sizes in Javanese Slendro" by Larry Polansky.

Manisrenga: [219.5, 266.5, 227, 233.5, 258.5]

Kanjutmesem: [224, 253.5, 237.5, 232.5, 264]

Udanriris: [255.5, 256.5, 223.5, 235.5, 234]

Pengawesari: [251.5, 233.5, 233.5, 236, 250]

Rarasrum: [229.5, 227.5, 253, 232, 261.5]

Hardjanagara: [216, 249.5, 216, 262, 261.5]

Madukentir: [268.5, 242, 243, 230, 221]

Surak: [206, 231.5, 238.5, 265, 264.5]

These are all in cents, and they're all somewhat close to the 240 cent step of 5-EDO, but they range from 206 to 268, and I think we can provide a finer-grained analysis than "equal-ish?".

These eight scales are all reach a total of 1204 or 1205 cents, except for Kanjutmesem which reaches 1211.5. I think that's pretty tight agreement.

The first five scales have intervals that, to my eye, seem easily split between a small ~230c and a large ~260c.

Manisrenga: [S, L, S, S, L]

Kanjutmesem: [S, L, S, S, L]

Udanriris: [L, L, S, S, S]

Pengawesari: [L, S, S, S, L]

Rarasrum: [S, S, L, S, L]

And indeed they all have 2 large intervals and 3 small intervals, but not in the same places. The Manisrenga and Kanjutmesem modes are the same in this representation, but the others are all distinct. The other scales have very small intervals of 206c and 216c, and/or medium sized interval around 242c, which sure stand in the way of a nice clean binary classification into 2 interval sizes. I guess I would describe them as

Hardjanagara: [vS, L, vS, L, L]

Madukentir: [L, M, M, S, S]

Surak: [vS, S, M, L, L]

In so much as there is some kind of intervallic structure here, which you could argue against, and in so far as all these scales can be represented as deviations from the previous (2 large, 3 small) structure, I'd guess that we have these identities

[S, S, S] = [vS, L, vS]

[L, S] = [M, M]

[vS, M] = [S, S]

These identifies let us define all the intervals in terms of e.g. the small interval and a comma interval, {c},

vS = S - c

M = S + c

L = S + 2c

We could also define all of them in terms of e.g. the large interval and the comma interval:

M = L - c

S = L - 2c

vS = L - 3c

Here are some cut offs that produce my categorization:

    L if 270 > interval > 247:

    M if 247 > interval > 238:

    S if 238 > interval > 220:

    vS if 220 > interval > 205

This categorization gives us average sizes of

vS ~ 214c

S ~ 231c

M ~ 241c

L ~ 259c

which gives us comma sizes of [17c, 10c, 18c] cents between successively sized intervals. Not so close! From this it looks more like

    S - vS = L - M ~ 18c

    L - S = M - vS ~ 28c

For an {a} sized comma of 18 cents and a {b} sized comma of 28c we would have:

M = L - a

S = L - b

vS = L - a - b

or

     L = S + b

M = S + b - a

vS = S - a

These definitions only work with the previous identities derives from [pseudooctave = 2L + 3S] if 

    

    2a = b

I guess that's approximately true? Like if you only have 8 cent pitch discrimination. But that just brings us back to these definitions

M = L - c

S = L - 2c

vS = L - 3c

I don't know, man. Maybe it's fine. For a pseudo-octave of 12.5 cents a Large interval of 259 cents, this gives us a comma value of 15 cents and these tunings for all the intervals:

L = 259

M = 244

S = 229

vS = 214

Yeah, it's fine. Those are exactly where they should be. No shame.

Here's a funny idea: if they've got a 15 cent resolution on their intervals, perhaps their scales are based on 79 or 80 equal divisions of a 1205 cent pseudo-octave. That is, dear reader, a ridiculous number of divisions to represent a couple of pentatonic scales that are basically all just 5-EDO. But if we go ahead with it, then

    L = 17 steps

    M = 16 steps

    S = 15 steps

    vS = 14 steps

Okay, so we fit a model to some data. Now what? Validate against more data! Polansky presents data for 8 more measured slendro scales, these measurements taken by Gadja Mada. These ones unfortunately aren't associated with regional names:

1. [237, 251, 248, 242, 258] # 1236c

2. [252, 239, 242, 236.5, 253.5] # 1223c

3. [237, 238.5, 232.5, 262, 238] # 1208c

4. [226, 252, 260, 234, 256] # 1228c

5. [232, 239, 248, 232, 259.5] # 1211c

6. [218, 238.5, 244.5, 244.5, 260] # 1206c

7. [238, 230, 257, 243, 250.5] # 1218.5c

8. [232, 234, 249, 251, 257] # 1223c

These have sharper pseudo-octaves, at an average of 1219c.

Using the previous cut-off values for categorizing intervals, we get these descriptions:

     GM_1: [S, L, L, M, L]

GM_2: [L, M, M, S, L]

GM_3: [S, M, S, L, S]

GM_4: [S, L, L, S, L]

GM_5: [S, M, L, S, L]

GM_6: [vS, M, M, M, L]

GM_7: [S, S, L, M, L]

GM_8: [S, S, L, L, L]

these scales are not only larger than the Kunst intervals in absolute tuning, they're larger than the Kunst by whole commas, with the exception of GM_3. The Kunst scales were all 79 steps in total, whereas these are variously [82, 81, 78, 81, 80, 79, 80, 81] steps.

Well, now what?

Now perhaps we admit that if all these regions have scales that differ by by twenty cents or more positionally, and they're all called slendro, then maybe slendro isn't that precise of an object. Maybe you don't need precise scales when you have inharmonic instruments. You can do whatever.

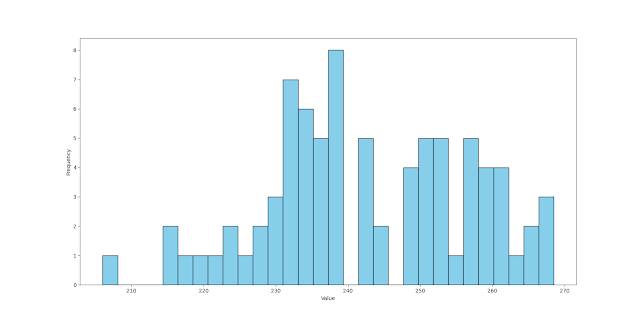
Here's a histogram of relative step sizes from Kunst and GM with 30 bins:

Is there anything to conclude from this? I tried to make a qualitative description and then checked how it looked at 40 bins and a lot of my description stopped being true. It's only a range of 60 cents. I think we could excuse people deviating from a desired interval size by 35 cents in either direction if they've got inharmonic instruments. And maybe some peculiarity of the inharmonicity is why all the octaves are stretched a little. Maybe it's just 5-EDO.

...